We follow up 'All the Radiators' with two questions on Liquid Droplet Radiators: How do we take into account inter-reflection in a droplet sheet? How does it affect the radiative efficiency?
Introduction to the task
Currently available calculators for the performance of liquid droplet radiators (LDRs) do not take into account inter-reflection between droplets.
They assume that the droplet sheet is only one droplet thick. They do not take into account the fact that some of the energy radiated by one droplet will be absorbed by an adjacent droplet.
We'll make several assumptions here:
-The droplets are perfectly spherical and can be perfectly formed down to 1um diameters.
-Droplets are nearly black (emissivity about 0.8).
-The droplet sheet have zero vertical variance and droplets are perfectly spaced.
-External effects are ignored.
With these assumptions, we can focus on the efficiency losses in droplet sheets.
It is known that regular radiators that radiate away waste heat, placed in close proximity to each other or facing each other, fully or partially, are less than 100% efficient. This is because some of the radiated energy is intercepted by the other radiator, an effect known as inter-reflection.
An emissivity rating of 0.8 also means an absorptivity rating of 0.8: Kirchhoff's Law of thermal radiation. This means a radiator that effectively radiates waste heat at a specific wavelength is equally effective at absorbing that wavelength.
All of these apply to droplets. When one droplet radiates away energy, it does so in all directions. Some of these directions are occupied by other droplets; they will absorb the energy and lead to a loss of overall efficiency.
We will now try to quantify this loss of efficiency.
A tale of two droplets
We will start off by considering two droplets in isolation.
The droplets will have the following properties:
-Diameter D and radius R
-An inter-droplet separation S
-An emissivity E
-A temperature T
Since we are dealing with small, hot droplets, usually of liquid metal, the values D, R and S will be expressed in micrometers (um, 10e-6 meters). E is between 8.0 and 0.99. T is in Kelvin.
From those properties, we obtain:
-Droplet surface area A
-Projected surface area P
-Radiative power emitted W
A and P are in um^2. The projected area is the surface area of a sphere, centered on a droplet, but with a radius equal to the separation S. W, in watts, is evenly divided across the droplet's surface area A. The projected sphere is how the droplet's heat is spread if we consider it to be radiating point source.
So, what do we do with all of this information?
Picture looking up at the night sky. How much of the sky does the Moon occupy? We are trying to answer a similar question with the two droplets. How much of one droplet's 'sky' is occupied by the other droplet?
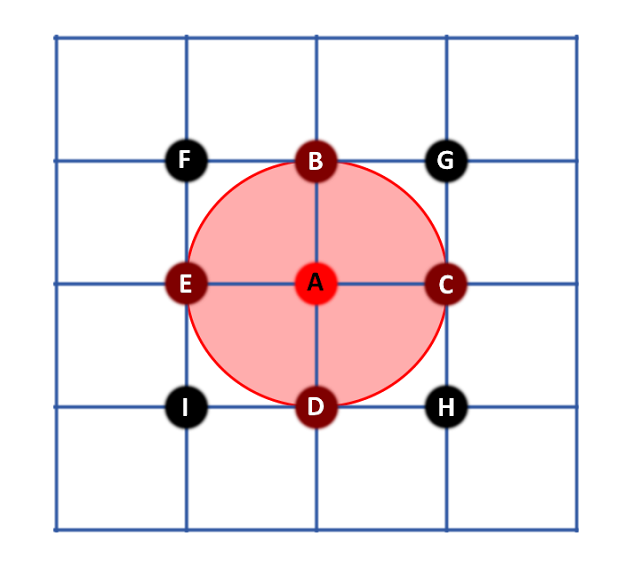
To work this out, we must first find out the surface area of the projected sphere at the second droplet's distance. Using the diagram above, generated by Geogebra's graphical calculator, we determine that droplet B's cross section, divided by the proected sphere's surface area, has the same ratio as the energy re-absorbed by droplet B divided by the total energy emitted by droplet A.
Droplets A and B have a diameter of 1um.
Both have a surface area of 3.14um^2 and a cross section of 0.79m^2.
The radius of droplet A's projected sphere is the distance A<-->B.
A<-->B = 0.5 + 10 + 0.5 = 11um
The surface area of the projected sphere is 1520um^2.
Droplet B occupies 0.79/1520 = 0.052% of droplet B's 'sky'.
So, we calculate that the inter-reflection between two droplets of 1um separated by 10um is so small as to be negligible.
Let's calculate the performance loss. We must take into account emissivity.
0.05% of each droplet's radiations are intercepted by another droplet.
80% of the inter-reflected radiations are re-absorbed.
Only 100 - 0.05*0.8 = 99.96% of the waste heat reaches empty space.
If we repeat the same calculations, but assume that the separation S is only 5 or 1um, then we get the following list of values:
Separation: 10um
Efficiency: 99.96%
Separation: 5um
Efficiency: 99.86%
Separation: 1um
Efficiency: 98.75%
What if we included even more droplets?
If we align a third droplet C, behind A and B, it will not absorb any radiations from A. It is in droplet B's 'shadow'. Droplet C has no effect on droplet A's efficiency, and we can suppose the same applies for any droplet in C's shadow and so on.
Using all this data, we can verify that the loss of efficiency caused by inter-reflection by adjacent droplets follows this equation:
R is the droplet radius, D is the diameter. S is the separation between droplets. If we input R=0.5, D=1, S=10 and E=0.8, we obtain 0.04%.
 |
| Droplets A and B. In grey, the droplet sheet's plane. In light red, droplet A's projected sphere. |
Droplets A and B have a diameter of 1um.
Both have a surface area of 3.14um^2 and a cross section of 0.79m^2.
The radius of droplet A's projected sphere is the distance A<-->B.
A<-->B = 0.5 + 10 + 0.5 = 11um
The surface area of the projected sphere is 1520um^2.
Droplet B occupies 0.79/1520 = 0.052% of droplet B's 'sky'.
So, we calculate that the inter-reflection between two droplets of 1um separated by 10um is so small as to be negligible.
Let's calculate the performance loss. We must take into account emissivity.
0.05% of each droplet's radiations are intercepted by another droplet.
80% of the inter-reflected radiations are re-absorbed.
Only 100 - 0.05*0.8 = 99.96% of the waste heat reaches empty space.
If we repeat the same calculations, but assume that the separation S is only 5 or 1um, then we get the following list of values:
Separation: 10um
Efficiency: 99.96%
Separation: 5um
Efficiency: 99.86%
Separation: 1um
Efficiency: 98.75%
What if we included even more droplets?
 |
| Droplets A, B and C are aligned and in the same sheet |
Using all this data, we can verify that the loss of efficiency caused by inter-reflection by adjacent droplets follows this equation:
- Loss of efficiency = [R^2 / (4*(D + S)^2)] * E * 100
R is the droplet radius, D is the diameter. S is the separation between droplets. If we input R=0.5, D=1, S=10 and E=0.8, we obtain 0.04%.
Sheet
A droplet sheet contains hundreds of thousands or even millions of droplets. We have assumed above that they are evenly spaced.
An even spacing of 10um requires that each droplet is separated from other droplets by at least that distance. Achieving this arrangement requires a specific 'tiling' of the surface area available: geometric tessellation can describe this tiling.
 |
| Regular, equilateral triangles with droplets at the vertices. |
The simplest to create is squares, but it is less efficient with its use of space. Tessellations with other geometric shapes are not able to pack as many droplets per square meter as the triangle or square.
To calculate the efficiency of a droplet sheet with each arrangement, we must consider each droplet within it's 'tile'.
Here is a triangular tile:
 |
| Droplet arrangement in triangle tessellation. |
Continuing our example from the previous section, each droplet is 1 micrometer wide and the separation distance is 10 micrometers, with an emissivity of 0.8.
The equation which determines the loss of efficiency between droplets A and B is the same as in the previous section. However, we must adapt it to take into account the fact that there are six droplets within droplet A's projected sphere.
[(6 * 0.5^2) / (4 * (1 + 10)^2)] * 0.8 * 100 = 0.25%
The loss of efficiency is six times greater at 0.25%.
Let's add the inter-reflection of the droplets H to S. We must note that droplets H, J, L, N, P and R are directly behind the first ring of droplets and therefore do not affect droplet A's efficiency. They are also twice as distant.
[(6 * 0.5^2) / (4 * (1 + 20)^2)] * 0.8 * 100 = 0.07%
We assume that third, fourth and further rings of droplets will have a totally negligible effect on efficiency. In a triangular tesselation, 1um droplets separated by 10um have an efficiency of 99.68%.
Here is a table of values for separations of 10, 5 and 1um:
Separation: 10um
Efficiency: 99.68%
Separation: 5um
Efficiency: 98.98%
Separation: 1um
Efficiency: 91.3%
For a triangular tesselation, the loss of efficiency equation for the first two rings is:
- Loss = [6*R^2/(4*(D + S)^2)+6*R^2 /(4*(D+2*S)^2)] * E * 100
 |
| Square tessellation droplets. |
Using the same equations as for the triangle tessellation, adapted for squares.
- Loss = [R^2/((D + S)^2)+ R^2 /((D+1.412*S)^2)] * E * 100
Using R=0.5, D=1, S=10 and E=0.8, we calculate a loss of efficiency equal to 0.25%.
Neglecting the influence of further droplets is justified as they only contribute less than 0.1% to efficiency losses.
Here is a table of values for separations of 10, 5 and 1um:
Separation: 10um
Efficiency: 99.74%
Separation: 5um
Efficiency: 99.13%
Separation: 1um
Efficiency: 91.6%
Efficiency: 99.74%
Separation: 5um
Efficiency: 99.13%
Separation: 1um
Efficiency: 91.6%
As for comparing between the two tessellations, you can pack twice as many triangles as squares into the same area. As the triangle has one less vertex than a square, this translates into 50% more droplets in the same area. However, creating the triangular arrangement requires a third nozzle in the droplet sprinklers.
200um droplets spaced by 1000um would suffer an efficiency loss of 2.86%, in a square configuration. This indicates that for small droplets with reasonable spacing, inter-reflection is a small influence on waste heat removal capacity.
Two sheets
What if we stacked two sheets of droplets on top of each other? This would double the number of droplets radiating. If the inter-sheet separation if equal to the inter-droplet spacing, then we could obtain a massive increase in waste heat removal capacity with only a small increase in the volume and equipment required.
 |
| Two square tiles in two sheets stacked above each other. |
 |
| Side view of the two droplet sheets as parallel planes. |
Let us calculate the efficiency loss for droplet A. We already have equations for the inter-reflection between droplets in the same sheet.
To continue with the previous examples, the droplets are 1 micrometer wide and separated by 10 micrometers.
Droplet J is directly above droplet A and is therefore separated by 10um. Droplets K, L, M and N are diagonal to A and the separation is 1.412 times greater; 14.12um. The remaining droplets O, P, Q and R are 15.53um distant from A.
Putting all these together, we calculate that K, L, M and N reduce efficiency by R^2 /((D+1.412*S)^2) * E * 100 : 0.087% and O, P, Q, and R contribute to a loss of R^2 /((D+1.553*S)^2) * E * 100 : 0.073%. Together with the losses due to same-sheet droplets, we obtain a total of 0.41%.
An efficiency drop from 99.74% to 99.58% is insignificant compared to a doubled output from having two droplet sheets instead of one.
Several sheets deep
So far, the efficiency losses have been nearly negligible, always less than 1%. What about droplets in the middle of a droplet cloud that is is dozens of sheets thick?
One might assume that the far greater number of droplets present in the cloud would create an obfuscating wall around the innermost droplets. Could it be that only the droplets at the edge of the cloud radiates effectively?
This is not the case!
Let's consider a droplet inside an a very thick cloud of droplets - perhaps 100 sheets deep or more.
Droplet shadows is a significant factor in this case - only the first droplet in a line of droplets absorbs radiations, all those in its shadow do not contribute to efficiency losses.
The most important configuration is an octahedron. The closest six droplets absorb more radiation than any number of droplets further away and are the biggest contributors to efficiency losses.
If we increase the number of sheets and droplets intercepted, we obtain significantly lower contributions to efficiency despite the increasing number of absorbing droplets. In the octahedron above, there are six droplets. In the cube below, 27 droplets are intercepting radiations but the innermost six droplets contribute
There are eight diagonal droplets per sheet intercepted, four at 1.412*S separation and four at 1.553*S separation for a total of sixteen.
It could be surmised that the loss of efficiency in a droplet radiator due to inter-reflection will depend on the number of droplet sheets and how many intercepted droplets they represent. However, a few calculations represent a simpler picture.
The projected sphere encounters more and more droplets as we increase the number of layers. Let's call the number of layers N. N is an always an odd number because we count the number of sheets above and below a central sheet. Therefore, N=5 corresponds to a cube of dimensions 4*S x 4*S x 4*S.
The number of droplets intercepted is 26 at N=3, 124 at N=5, 342 at N=7 and 728 at N=9. This indicates that the intercepted droplets follows a patterns of [(N)^3 - 1].
The number of new droplets is we encounter as N rises is actually smaller. It should follow an [(N^3 - (N-2)^3)] pattern; basically, the difference between the larger and smaller cubes from 2-sheet steps.
At N=5, there should be 98 new, at N=7 there'll be 218. This is a much slower progression.
Finally, we must find out which of the new droplets are shadowed behind the previous droplets. We can find this simply by deducing the number of new droplets by the number of new droplets from the previous step.
For example, if I wanted to calculate the new non-shadowed droplets in a droplet cloud 7 sheets deep (N=7) compared to a cloud five sheets deep (N=5), I'd first need to know the number of droplets creating shadows in N=3.
This creates a series. It is best to use an Excel sheet to handle series, as they cannot be properly represented by an equation:
N=3 gives 26 shadows. N=5 has 98 new droplets. 98-26: 72. So, N=5 creates 72 new shadows. For N=7, we calculate 218 new droplets. We deduct 26 shadows from N=3 and 72 shadows from N=5 for a total of 120 new shadows.
How do we use the number of shadows?
Well, we can estimate the efficiency of a droplet radiator as the number of sheets increases. In a cubic tessellated volume, in other words a grid, the distance between a radiating droplet and an inter-reflecting droplet in a sheet N is at a minimum equal to S*N, at a maximum at 1.553*S. S*N represents a droplet directly above the radiating droplet. 1.553*N represents a droplet absorbing radiations from the corner of a cube.
Any other position occupied by any droplet is further away than S*N or closer than 1.553*N*S.
Using these distances, we can restrict the range of efficiency losses caused by inter-reflected at any number of sheets.
Inter-reflection efficiency loss estimates
At a distance S*N, a droplet covers a percentage of the radiating droplet's sky equal to (R^2)/(4*(D + S*N)^2)*E*100.
We multiply the percentage by the number of new shadows to obtain the maximum losses caused by the droplets in the sheet.
At a distance S*N, a droplet covers a percentage of the radiating droplet's sky equal to (R^2)/(4*(D + 1.553S*N)^2)*E*100.
We multiply the percentage by the number of new shadows to obtain the minimum losses caused by the droplets in the sheet.
Here is a table of values for the percentage of efficiency losses caused by droplets of 1um diameter with a separation S=10um and an emissivity of E=0.8.
We find that the biggest contributors to efficiency losses are the first few sheets. Despite the increasing numbers of droplets, sheets further away contribute less and less to inter-reflection losses. Even at 100 sheets, losses are at 6%.
Here is a table of values for the percentage of efficiency losses caused by the same droplets above separated instead by 5um.
We see that the losses are quite a bit more significant. The increases in inter-reflection start petering out after 50 sheets, with the next 50 sheets contributing only 3% to the accumulated average losses. Losses are offset by the droplets being packed 8 times more densely.
Here is a table of values for the percentage of efficiency losses caused by the same droplets above but separated now by 1um.
An accumulated average of over 100% means that all of the radiating droplet's radiations are blocked and absorbed by the surrounding droplets. At 9 sheets deep, we can confidently say that the central sheet contributes nothing towards the droplet cloud's performance.
Do note that these tables are calculating the efficiency of the innermost sheet only. The average losses once sheets closer to the edges of the droplet cloud are considered is lower than what the accumulated average suggests.
Conclusions
For properly spaced droplets, where the separation is much greater than the droplet diameter, the efficiency losses caused by inter-reflection is quite negligible.
However, for densely packed droplet clouds, inter-reflection becomes a significant issue that greatly reduces output despite the greater number of droplets.
 |
| Most illustrations of liquid droplet radiators depict them as rather thick and not one sheet thin. |
This is not the case!
Let's consider a droplet inside an a very thick cloud of droplets - perhaps 100 sheets deep or more.
Droplet shadows is a significant factor in this case - only the first droplet in a line of droplets absorbs radiations, all those in its shadow do not contribute to efficiency losses.
 |
| Imagine the expanding spheres as the radiating waste heat, with the horizontal lines representing droplet sheets. |
 |
| The droplets intercepted at one separation. The projected sphere is three sheets tall. |
 |
| Here, we have included the diagonals, which form a cube around the previous octahedron. |
 |
| A section of the droplet cloud. |
The projected sphere encounters more and more droplets as we increase the number of layers. Let's call the number of layers N. N is an always an odd number because we count the number of sheets above and below a central sheet. Therefore, N=5 corresponds to a cube of dimensions 4*S x 4*S x 4*S.
 |
| 4x4x4 cube in isometric view. |
The number of new droplets is we encounter as N rises is actually smaller. It should follow an [(N^3 - (N-2)^3)] pattern; basically, the difference between the larger and smaller cubes from 2-sheet steps.
At N=5, there should be 98 new, at N=7 there'll be 218. This is a much slower progression.
Finally, we must find out which of the new droplets are shadowed behind the previous droplets. We can find this simply by deducing the number of new droplets by the number of new droplets from the previous step.
For example, if I wanted to calculate the new non-shadowed droplets in a droplet cloud 7 sheets deep (N=7) compared to a cloud five sheets deep (N=5), I'd first need to know the number of droplets creating shadows in N=3.
This creates a series. It is best to use an Excel sheet to handle series, as they cannot be properly represented by an equation:
N=3 gives 26 shadows. N=5 has 98 new droplets. 98-26: 72. So, N=5 creates 72 new shadows. For N=7, we calculate 218 new droplets. We deduct 26 shadows from N=3 and 72 shadows from N=5 for a total of 120 new shadows.
 |
| Seems to be 11 sheets thick. |
Well, we can estimate the efficiency of a droplet radiator as the number of sheets increases. In a cubic tessellated volume, in other words a grid, the distance between a radiating droplet and an inter-reflecting droplet in a sheet N is at a minimum equal to S*N, at a maximum at 1.553*S. S*N represents a droplet directly above the radiating droplet. 1.553*N represents a droplet absorbing radiations from the corner of a cube.
Any other position occupied by any droplet is further away than S*N or closer than 1.553*N*S.
Using these distances, we can restrict the range of efficiency losses caused by inter-reflected at any number of sheets.
Inter-reflection efficiency loss estimates
At a distance S*N, a droplet covers a percentage of the radiating droplet's sky equal to (R^2)/(4*(D + S*N)^2)*E*100.
We multiply the percentage by the number of new shadows to obtain the maximum losses caused by the droplets in the sheet.
At a distance S*N, a droplet covers a percentage of the radiating droplet's sky equal to (R^2)/(4*(D + 1.553S*N)^2)*E*100.
We multiply the percentage by the number of new shadows to obtain the minimum losses caused by the droplets in the sheet.
Here is a table of values for the percentage of efficiency losses caused by droplets of 1um diameter with a separation S=10um and an emissivity of E=0.8.
Here is a table of values for the percentage of efficiency losses caused by the same droplets above separated instead by 5um.
We see that the losses are quite a bit more significant. The increases in inter-reflection start petering out after 50 sheets, with the next 50 sheets contributing only 3% to the accumulated average losses. Losses are offset by the droplets being packed 8 times more densely.
Here is a table of values for the percentage of efficiency losses caused by the same droplets above but separated now by 1um.
An accumulated average of over 100% means that all of the radiating droplet's radiations are blocked and absorbed by the surrounding droplets. At 9 sheets deep, we can confidently say that the central sheet contributes nothing towards the droplet cloud's performance.
Do note that these tables are calculating the efficiency of the innermost sheet only. The average losses once sheets closer to the edges of the droplet cloud are considered is lower than what the accumulated average suggests.
Conclusions
For properly spaced droplets, where the separation is much greater than the droplet diameter, the efficiency losses caused by inter-reflection is quite negligible.
However, for densely packed droplet clouds, inter-reflection becomes a significant issue that greatly reduces output despite the greater number of droplets.








This is actually interesting. A radiator shaped like a cube or cylinder is much more compact compared to a standard "wing", and the shape of the ship can be more compact as well. This may not save much on mass, but a compact ship should be much easier to manoeuvre without large booms or radiators.
ReplyDeleteAnd of course colonies and other structures may benefit from this as well.
Quite true. In the 10um spaced radiators, you can get clouds of several hundreds of sheets thickness and suffer only about 7% inter-reflection losses. It would still be less than a centimeter thick and yet it would pack so many more droplets.
DeleteThe best part is that you'd only have to use a single spraying and collecting arm.
I think there is one factor that you overlooked: you take into account the energy that is being asorbed by other droplets, but I do not see anywhere where you take into account the increased emission by those other droplets.
ReplyDeleteRemember that emission is dependent upon temperature. When a droplet absorbs energy from neighboring droplets, it effectively increases the temperature of that droplet... and the emission increases at a factor of T^4 with temperature.
Of course, factoring this in would probably require factoring in specific material used for the droplets. This is because the actual temperature increase would be dependent upon the heat capacity of the material.
Something to keep in mind: the situation we are describing is essentially exactly what happens when dealing with a solid or liquid material. Note that the blackbody radiation of a material is independent of its thickness. The situation would be different if there were a hot core layer that is trying to emit through cooler outer layers (a situation equivalent to wrapping a blackbody source with an insulator), but as is, we are dealing with an essentially homogenous heat source.
What is actually critical is that the given available radiative area will be a constant. To a certain extent, the density of the droplets will be low enough that the system will act AS IF it were a monofilament, regardless of how thick it actually is. However, there is a limit (specifically, the number of droplets you would actually be able to fit into a real monofilament sheet) beyond which you are no longer creating greater emissive area by adding more droplets. This would then be the equivalent of just making a thicker blackbody: same emission per surface area exposed, but more mass.
Quite right, more steps would be required to work out the 'effective' efficiency of a droplet radiator when we consider that 'inefficiency' can be translated into droplets staying hotter for longer.
DeleteIf we take the case of a 93% efficient radiator, then each droplet eventually re-absorbs 7% of the energy it emitted (after bouncing back and forth between not-perfect-blackbody objects).
A simple fix would be reduce the emissivity.
A single droplet might have an emissivity of 0.8, but inside the cloud the effective emissivity would become 0.73: this would account for efficiency losses while allowing us to use a straightforward drop in temperature.
Looking at the entire radiator as a single object, we can look at it from any direction, choose any single point too look at and see if there is a droplet radiating toward us there.
ReplyDeleteThe two extreme examples are an empty radiator with no droplet, where no point radiates, and the full radiator, who is so dense that any point radiates. The second one is equivalent to a solid radiator.
As such, it should be possible to describe any droplet radiator configuration (droplet size, distance, positioning) and assign it a solid radiator equivalent percentage.
This only works for perfectly distributed droplet clouds where all droplets maintain a distance S from each other. This allows us to scale up and down their density of distribution seamlessly.
DeleteIn a random distribution, some droplets are closer, others father, and the distances average out. However, droplets closer to each other are disproportionately inefficient compared to how much more efficient droplets farther away from each other are: the efficiency losses do not average out like distances do.
Nonetheless, it is a nice idea that might be worked into a calculator.
I am not necessarily saying that there would not be ANY loss of efficiency due to droplet absorbtion. However, I suspect that any such loss would be much lower than your initial projections.
ReplyDeleteAgain, once you have more droplets than the number that you could actually fit into an actual monofilament sheet, there WILL be a definite loss of efficiency, equivalent to having a thicker blackbody block.
Agreed. That would be the maximal practical density of droplets in a sheet.
DeleteA design idea I ran across on Worldbuilding Stack Exchange, which covers many of the ideas talked about on this blog, but with some interesting twists:
ReplyDeletehttps://worldbuilding.stackexchange.com/questions/12354/what-would-a-space-fighter-look-like
"I think that a space fighter would in a way act more like a submarine than a modern warplane. Paint the thing black and it'll be hard to see. It'd be shaped to scatter radar reflections in all directions, since aerodynamics would be unimportant. Think of an anechoic chamber turned inside out. And anything emitting radar would be making itself much more visible than the target (of course, the radar emitter could be on a drone, but then the fighter could be a drone too).
It'd want to keep its heat signature down, because that's always going to be broadcasting its location to passive sensors. I'd imagine a liquid droplet radatior with deployable arms, and using a railgun with explosive projectiles as its armament. The explosives wouldn't be to make a bigger hole in the target, but to turn the projectile into shrapnel for a better chance at a hit.
Also, presenting more mass toward the likely location of the enemy would serve two purposes -- one, as armor of a sort, and, two, it'd be nice if that could be used to shadow the radiators from enemy heat sensors. We might as well keep the propellant there, as water or hydrogen slush.
So, I'd say a spiky mushroom with a long stem, periodically with what appear to be wings sprouting up behind the head when it seems safest to deploy the radiator."
Using multi layered droplet curtains allows for smaller radiators behind the "mushroom cap", but the "stem" might have to be shielded by dielectric mirrors to reflect the IR radiation away from the ship.
Somewhat related is the newest entry in Atomic rockets: In-A.22 Nikto-ega class interceptor.
http://www.projectrho.com/public_html/rocket/realdesignsfusion.php#niktoega
A pulse fusion ship designed to carry a brace of (presumably) NEFP missiles, and having a secondary particle beam weapon as a CIWS looks a lot like the "Firestar" concept. While I am somewhat dubious of the author's projected employment of the ship, tactics are dependent on your assumptions. I would think of a Firestar built along these lines as being part of the outer layer of a constellation or moving in independent battlegroups, but YMMV.
I think the importance of detection and defense are reversed in the quoted comment.
DeleteThe space fighter being described is no Hydrogen Steamer. It will have surfaces bright and hot enough to ensure detection through passive emissions alone, something an 'anechoic chamber turned inside out' won't help with.
Droplet radiators are also very hard to hide from any direction. You'd have to use something like a membrane covering all the droplets, half opaque and half transparent... but you'd run into the problem of cooling down the opaque half. This is ignoring the fact that it is very simple to place sensor behind your spaceship and get a strong signal from the exposed side.
Since detection is so hard to avoid unless we rely on very specialized designs or plot-dependent situations, it is better to rely on defense. This means concentrating armor at your opponent. A spinning, sharp cone has the highest defensive capability per kilogram against lasers. A layer of reactive armor plates is most efficient against high velocity projectiles.
If we place the radiators edge-on behind the widest point of the cone, we'll end up with something like a flechette shape. Bonus points for looking cool.
Interesting. I'm currently brainstorming for a far future space opera setting with some hard sci-fi elements so the shape of the warships is of a particular issue.
DeleteI have imagined the lead ship to look like a spike with a ring around its base- that would be the habitable section that would retract (and stop spinning) during combat.
My question is- can a liquid droplet radiator be enclosed around armor so it would act as sort of an internal coolant protected by the hull? Can the radiator emissions be redirected as part of its fusion drive exhaust?
Hi John! I'd be glad to assist you.
DeleteArmored nose cone, rotating ring for habitation, sounds good so far.
Radiators need exposed surface area to remove heat from their coolant flow. Enclosing them in armor is counterproductive. Fusion exhaust is much much hotter than any radiator's coolant fluids, so since heat will move down a temperature gradient, the effect will be contrary to what we want.
What I would suggest is to use plasma wings held in place by magnetic fields extending beyond the hull. The plasma holds tiny particles within it. This is the basis for dusty plasma.
The dusty plasma can circulate the particles in a loop from a heat exchanger to the vacuum of space to cool them down, and back again. The plasma wings will give you a great freedom of choice for the shape of your hull.
Shooting these plasma wings is like shooting a cloud. You'd need massive amounts of energy to disperse it, and then it can be recreated with a few grams of material. Convenient!
Wow, thanks! I never thought if it that way. I'm assuming that these plasma wings will glow from the radiation, giving it the effect of looking like wings made of energy, am I right? If that is the case the ship designs would resemble birds, butterflies or even the old sailing ships!
DeleteCould these plasma wings be used for defense against lasers too?
It is unlikely that the plasma wings will be of much use against lasers. The particle densities will probably be MUCH too low (by several orders of magnitude). However, I suggested somewhere (I don't remember if it was here or not) that a similar sheet of metallic sand might be useful, in a similar arrangement. The "sand" could be semi-bound through even micro-g attraction, surface tension, etc; and could be reinforced through the use of electric currents and/or magnetic fields.
DeleteEven better might be to suspend the "sand" in a high-viscosity gel, to allow more fluid motion. The main idea is that these layers can be much more easily reinforced in case of attack. You would probably get a burn-through of considerable depth, but it would be easier to recapture fragments, and fill-in burn-through holes/craters. There would therefor be much reduced opprtunity for the enemy to take advantage of burn-through from previous beams.
Thanks, Mikkel! Excellent point. My question is would it be possible to "shape" the metallic sand (either through advanced magnetic fields or nanites) into an outer bubble to cover the entire ship's hull like the shields they have in Star Trek?
DeleteThe same flux-pinning used for the flux-pinner superthermal radiator concept (see the 'All the Radiators" blog post) can be made to hold metallic sand in place.
DeleteHowever, such a shield is useful only if you want to replace armor depleted by an attack or if the magnetic fields holding the particles in place is greater than the electrostatic forces holding the particles together if they were a solid. If it is the not the case, it is better to just use segmented solid plates that physically shift to cover gaps.
Basically, unless you have magnetic field strengths of thousands of Tesla, then it is better to just use solid plates.
@John Triptych,
DeleteHaving it cover the outer hull would not be a problem. However, there are certain drawbacks to covering the entirety of a hull. Among these arethe need for certain items to be exposed in orderto function properly, and the mass involved in trying to cover everything.
@Matter Beam,
Yes, solid matter holds together much better. However, it is also that much more difficult to repair, and to move around. In short, it is much, much easier to take advantage of burn throughs in solid matter, and much more difficult to fill in these burn throughs.
Another issue is that being held together is not actually that much of a deterent against lasers (it is far more useful against kinetic weapons).
A good compromise would be to alternate layers of solid shielding with "sand" shielding.
Got it! So a hull with multiple layers of Whipple shields that can move around and in between will be fields of metallic sand. This is awesome.
DeleteSo it looks like I've got the ship defenses thought out, now on to the weapons! Thanks, all.
You probably ARE going to want at least one layer of actual solid shielding. Notably, this will be part of what naval designers call a "citadel", which is a "box" of armour surrounding the most important parts of the ship (it does not cover bow, stern, or superstructures). Whether part of a citadel or not, the solid armour would be necessary to protect against explosive shells. While sand and whipple shields might be sufficient protection even against ultra-high velocitiy kinetic projectiles that tend to distribute energy inward (as do explosive penetrator rounds, which are NOT the kind of explosive shells I am talking about here), an explosive shell is designed to partly pentrate into armour before it explodes. In this case, the explosion creates a LOT of lateral force that is meant to widen gaps in armour, as well as outward force that will rip armour away. Sand and whipple shields are fairly useless against such traditional shells.
DeleteFor an idea of how to put this together, I suggest you search "Iowa class battleship armour arrangement". The Iowa class had an outer skin, as well as four separate interior hull shins (sometimes labeled as "SHD", numbered 1-4 moving inward... and NOT including the outer skin). Each of these hull layers had a "void" between them, some of which were used as fuel storage or drinking water storage. SHD#3 was the armour plate, and SHD#4 was mostly to catch spalling. I would suggest a similar arrangement, replacing SHD#2, SHD#3, and the void between as the zone for alternating "sand" and whipple shield layers. The outer void (void#1) would be filled with water (or water ice), and the outer skin would be a lightweight solid armour layer.
Note that what I am suggesting here would be a warship design. It would be much too heavy for a stealth craft, although it would probably integrate some stealth features, mostly to make it more difficult for accurate targeting.
Smaller vessels and craft would more likely rely on manoeuverability for protection. Although lasers can move quickly, it is extremely difficult to move them precisely at great distances.
From re reading the comment, the author is obviously looking at the idea of making the ship difficult to "see" in the microwave/radar spectrum, and painting it black should make it difficult to see in the visible light spectrum.
ReplyDeleteOf course, making it invisible in the infra red spectrum is not being considered at all in this design. The only thing that I could think of to make it more difficult to target is placing a metamaterial "shield" in front of it which refracts IR radiation. An umbrella shaped shield held in front of the craft and designed to refract IR radiation in a large open "cone" (think of the cones used around an animal to keep them from scratching themselves) would provide a rather strange"view" to any IR target seekers coming from the frontal arc. Like most things, this is not a 100% solution, and in the sorts of space battles where the sky is fun of target seeking drones and SCoDs (not to mention laserstars) this would not provide a great deal of protection at all.
Refracting the IR emissions still means that some percent of the emissions end up straight in the enemy's CCD sensors. A statistical analysis of the concentration and distribution of 'hits' on the sensor's pixels will give a 'soft detect' of any target, as described in Stealth in Space is Possible IV.
DeleteWhat the metamaterials could help with is avoiding a long-range 'target lock' using passive sensors only. A laser beam would have to be focused on your ship, forcing your enemy to in turn reveal themselves.
In modern stealth tech, you actually don't want to scatter radar in all directions, as this allows detectors in any irection to pick up the radar energy. No matter how weak that energy is, there are means to detect that energy if it comes in your direction. Of course, there are both benefits and detractors with any given tactic for detection, so picking the wrong one could easily cause the energy to be missed... but this is straying from my point.
DeleteModern stealth, does not shape forms to radiate energy in all directions, but to radiate in specific directions away from the source. The first step is to use mostly flat forms in such a way that incident angles naturally reflect the energy away from the source, except when that source is emitting orthagonally to the reflecting plane... wherever possible, the planes are then angled so that any such orthagonal points are in places where interception (if detection does occur) would be difficult. From here, the forms are further shaped to bounce the reflected signal in such a way that it is virtually impossible to get an orthagonal angle to a surface. For example, the SR71 used concave triangular sections to direct radar away from a source in controlled directions.
There are, of course, stealth techniques designed to scatter radar. However, these are used in radar absorbant materials that scatter the signal INTERNALLY. This spreads out the radar return signal over time, preventing accurate ranging. This is also combined with shaping so that when the signal energy IS emitted, the emission can be directed, in a controlled manner, away from the source signal.
The problem with trying to find a neat-cut solution to how to respond to incoming energy and how to handle outgoing emissions is that it crashes head-on with the obstacle that is author choice.
DeleteFor example, in a setting where the two opponents start far away from each other and everything behind the space forces is 'safe', we can imagine an artificial horizon where radiating in front of you is bad and radiating behind you is safe.
That sort of thing lends itself to directional radiator and hulls shaped to deflect RADAR and LIDAR in one direction instead of another. It is the situation we live in, where there are multiple horizons, both natural and artificial.
However, an author can just as easily create a setting where sensors are all over the place, or everyone has allies and neutrals reporting the position of the space forces. There is no horizon, the enemy can be looking from anywhere and attack from a wide range of directions.
This time, directional tactics would not be very useful, as you cannot know where to point your emissions if you don't know where the enemy is, and you cannot know where the enemy is without revealing your own position. So, it is best to simply reduce your emissions to gain some level of surprise on strategic scales (where did your mid-course burn move you?) even if you cannot hide you on tactical scales (evading a missile lock).
It appears that might original reply to this got lost, so here it goes again.
DeleteFirst: stealth never relies on absolutes. There is ALWAYS a non-zero chance of detection. Thus, even though there is no guaranty that there will be no one in the direction of reflection, those who employ stealth will still take the risk.
There are actually a number of factors that are taken into consideration. These include probable placements, known or projected sensitivities/signal strengths, etc. radiating in all directions might be prefered if you KNOW that enemy platforms have a given sensitivity that you KNOW is above the reflection amplitude at a given intended range of operation. However, far more often, planners will opt to take chances on minimalised windows of peak reflection, in exchange for virtually no reflection in other directions.
Second: you are quite correct that it is not possible to be certain where all the detection platforms are going to be. But that works in both scenarios. You never know how close a platform is going to be, either, and detectability is a function of distance (among other factors, of course). The one thing you CAN be certain of: if you reflect at all angles, you WILL be reflecting toward at least one detector platform, including the source... and that can be very bad.
Third: you ABSOLUTELY do NOT want to reflect toward a source. If the source can detect the reflected signal, the enemy will have presence, direction, AND range information... possibly velocity as well. However, if a non-source detector DOES receive the reflected signal, all it will have is presence, and a more or less accurate estimate of direction. It will have zero range info.
(TBC)
(cont)
DeleteFourth: "all over the place" is relative. In terms of resources, it is highly unlikely that it would be possible to establish a network of platforms of the size you suggest. It is PHYSICALLY impossible to establish a network that would be able to detect an asset regardless of reflection angle, with no gaps.
Let's assume that an asset has an unreasonable reflection scatter of 1°^2 (that is, the peak, or near peak, energy levels will be as strong 1/2° off the norm as it is along the norm itself). You would already need over 40 000 platforms surrounding the asset, WITHIN detection range, for a given location in space (these platforms will have to cover every square degree projected from the asset). The problem is, as the asset drifts from the geometric centre of this array, there will be gaps to exploit... to say nothing about assets that are outside this array. The asset will be detectable only so long as there is a detector in EVERY 1°^2 window.
(TBC)
I will answer your points. I must apologize for not always responding to the comments you have sometimes made on Google+ or on this blog.
DeleteI must note that reflecting a signal from an enemy's active sensor will only be a small part of the detection game. Only two likely scenarios involve handling an incoming signal: a hard target lock for weapons fire after a strong confirmation of your location and identity has been obtained through passive sensors, or if the enemy if blindly waving a laser around like a flashlight without fear of being attacked by any number of 'silent' passively-sensing opponents.
In the first case, throwing off the active sensor's signals will only lead to a worse targeting solution. In the second case, we would be dealing with a very assymetrical conflict where being detected is the least of your worries!
The scatter numbers you have selected for the example in your second comment seem unrealistic. Active sensors will use RADAR of long wavelengths or LIDAR of short wavelengths.
A signal that reaches your spaceship will continue expanding at an equal rate after you bounce it off in another direction. This means it could cover a very large area (spot size) after a certain distance. The critical point I'd like to made is that after a certain distance, the reflected signal will cover the entire hemisphere of some sensor, even if that distance is several AU.
But, even at that distance and after the signal has been spread out, it will likely remain detectable by sensors of the level of sensitivity needed to detect passive IR emissions.
A quick calculation tells me that a 10MW LIDAR beam is detectable by 10e-17W/m^2 sensors even after it has been spread over an area 1.12 billion km in diameter. What distance this corresponds to depends on the sensor's LIDAR array, but even for a small 1m wide mirror and 400nm wavelength beam set-up it is 1.15e15 meters... that's over 7800 AU and well outside the solar system. Can you ensure that there isn't a single sensor within such a massive cone?
I had intended to continue my previous message, but I will elay that for a bit in order to address your recent response.
DeleteFirst, bringing the discussion back into context, in this particular thread I was pointing out that the favourable strategy would be to risk projecting a higher peak reflection in (a) limited direction(s), rather than to risk diffusing the signal over all directions (absorbing the signal and diffusing it over time is not being considered, as the stategy can be applied to either technique). Actually, given your values for a 10MW LIDAR, you actually support my argument somewhat, as it would suggest that (for reasonable ranges, at least), any return at that source strength, no matter how deffuse over area, would easily be detected... including by the source platform.
That said:
The second thing I would like to mention is that you are not looking at the appropriate figures. Yes, the area of the window you describe is quite large (although, as I will explain shortly, not QUITE as large as you indicate). However, you are failing to take into consideration exactly how astronomical the scales we are dealing with actually are.
I ran the numbers over in my head, so feel free to double check. However, the following are some important contexts, assuming your own calculations are accurate (I have no reason to doubt them):
*1 billion+ km IS a rather sizeable swathe of space. However, this window is actually only on the order of 1/10^7 of the projected sphere of 7800 AU. A little more accurately, you would need upwards of 130 or 140 MILLION platforms to cover each of the windows of this size, rather than the 40 thousand I was originally estimating. I think this works out to an actual angular window of a bit under 1/40°^2, rather than my assumed 1°^2.
Please note, when I did these mental calculations, I was using the (mis-remembered) distance figure of 7600 AU... at 7800 AU, you might need a few thousand more platforms.
*1 billion km is indeed the likely order of magnitude for the original source beam. However, at this spread, the beam will already be at 112 km diameter by the time you reach a distance equivalent to half the distance between the Earth and the moon. Even with a target with a cross section as large as 1 km (roughly, IIRC, the size of an Executer class super star destroyer, illuminated full flank), the reflected energy will only be approximately 1/12 000th of this value. The energy density will progress unchanged, but this means the actual reflected cone will only be on the order of 1% the radius you calculate. The vast majority of the actual cone projected will be the unhinderedsignal from the source itself. BTW, this means that there is a fraction of a % chance that a reflected signal will be indistinguishable from the source signal, unless the receiver knows EXACTLY where the source was, and the exact direction of transmission, when the signal was sent.
I see. You're going for a high-risk either I'm detected or not approach to detection.
DeleteIn the best case scenario, your opponent pings you with a LIDAR beam and you bounce it off into an empty corner of space. Because it is so hard to cover all the areas, the reflected signal is never intercepted.
The calculation I did was [(10e7/10e-17)/3.14]^0.5*2. It gives the diameter.
There are multiple problems with this scenario. I'm not saying it will never happen or that it is even unrealistic to assume that it is actually the likely and expected outcome. These are just ideas a military planner would suggest to prevent this situation from benefiting opponents.
The first is the ability to bounce a LIDAR signal within a very very confined cone. By definition, the incident radiation is reflected at the same angle and spread: if you are pinged with a narrow, focused beam, the reflection can be pinpointed in another direction. If however the incoming beam is a broad RADAR wavelength, how can you be sure that the signals you are bouncing won't spread out so much that they'll be intercepted on the way back? This is especially problematic when 100MW lasers implies a 100MW+ output from RADARS.
There's also the problem with geometry and materials.
Is there even a material that can interact equally well both RADAR and LIDAR and all the frequencies in between? There are existing materials that can handle radio, microwave, infrared ect... but can you put them all together in the same reflecting face without interfering with each other?
Let's assume such a material exists. Let's also assume that you need to bounce the incoming signals a full 45 degrees of more to the side to prevent a broad beam from spreading out on the way back to the opponent.
The geometry becomes problematic. You will able to handle signals coming in from the intended direction. What about signals coming in from other directions? What about two directions at once? How well can you handle a pencil-wide beam that can catch an exposed corner on the hull or a sensor shroud, lighting you up like a Christmas tree, and at the same time deflect RADARs with wavelengths longer than the entire spaceship?
If we do a calculation for a sacrificial 'sonar buoy'-type sensor platform that pulses 100MW LF-band radio emitted by a 10m wide phased array, we find that a 10e17W/m^s cheap sensor (more expensive sensors will have 10e-19 or better) will detect a signal after it has been spread out over a disk 3.56 billion km in diameter. The LF radio signal reaches this size after travelling 29.2 million km, so at a 14.6 million km distance from the target. You'll notice that the separation between the you and the platform is much smaller than the diameter of the disk - it is unescapable unless you somehow manage to deflect the signals by more than 180 degrees!
Finally, the problem with distinguishing between your own signal and others can be simply solved by scanning your output over a specific range of wavelengths or pulsing it in a specific patterns or using more advanced modulating signals from AESAs.
I might have to break up this response.
DeleteThe calculations you were using are self-evident. I believe I already said that I had at least confirmed the order of magnitudes when I calculated the figures in my head. However, I think one of us might be miscalculating for the 400nm LIDAR divergeance figure. On the one hand, if my calculations are correct, the range for LIDAR would actually be MUCH greater. On the other, the divergeance angle would be much smaller.
I am using the formula Total Divergeance (radians) = 2 * wavelength / (pi*waist). Multiply this figure by 57 to get the value in degrees.
Sorry, gotta go. TBC.
I got that number from the Laser Weapons Calculator, but I might have made a mistake.
DeleteI'll await the rest of your response.
(CONT)
DeleteSo... to estimate the total divergence, assuming a waist of 1m, multiply the wavelength by 38 (2*57/3). For a 400 nm LIDAR, this comes out to about 1.5*10^-5°, or 0.000015°. This is quite a bit less then the 1/20° that I originally estimated from your figures, although that might be the result of miscalculation on my part.
Moving on, however, you are quite correct that there is much greater risk from divergence at RF frequencies. Notably, at around 26 mm RF, the divergence from the proposed 1m transmitter works out to the 1° figure that I originally proposed. At 0.05m, the window of reflection increases from 1/40 000th of the full sphere to 1/10 000. At 0.5m, chances of detection by a single receiver increases to 1%. So, yes, there is definitely a risk with RF frequencies.
I will get back to that shortly.
This, however, assumes a waist of 1m. The problem is, once the emitted beam is large enough to cover the entire cross section, the area of the reflecting surface becomes the new waist. This means that you need togo to a 500m wavelength in order to have that 1% chance of detection by a single window.
That said, it is highly unlikely that we will be dealing with "stealth" assets that large. Therefor, we will assume the significant risk factor when getting into the range of millimetric RF.
OTOH
I am glad that you mention the issue with material.
There are three basic ways that photons interact with matter. Reflection, absorbtion, and transmittance (translucense/transparency).
As far as reflection is concerned, the difference in material does not change the property of divergence. Divergence will depend only upon wavelength and waist. Now, there IS the issue of reflective diffusion. However, this is not so much a matter of material used as it is a matter of how that matterial is configured. If you have a very grainy surface, the sizes of the grains essentially replace the waist values of the surface area. This means that it would be desirable to carefully polish the surfaces of the stealth asset.
The reflectivity of the material DOES become important, however. As it happens, as RF photons approach millimetric wavelengths, and especially as they approach increasingly longer wavelengths, most materials lose their ability to reflect the photons. So long as you avoid metals, the vessels will essentially become transparent to these longer wavelengths. Thus, significantly less energy available for detection. There is aso the possibility that some of the RF energy will be absorbed, rather than transmitted, so we are not necessarily dealing with transparency... but the end result is that there will not be sufficient reflected signal at these wavelengths.
SO... you increase the source strength.
Bad idea. Probably.
As it happens, amplitude of the signal is ALSO important. It is possible to chart out the reflectivity of a material according to the amplitude of the signal. In general, as the amplitude increases, reflectivity decreases. For a while, this graph will be almost flat, with a negligible decrease in reflectivity. However, all materials have a region, refered to as the plasma barrier, where the reflectivity drops off sharply (in aluminum, for example, this occurs at about 18mV, IIRC). This is usually followed by anothehr region, known as the band gap (IIRC), where the energy is absorbed rather than transmitted. Interestingly, this does NOT mean that you have a plateau in reflected energy. It means that if you trnsmit too much energy (you cross the threshold into the plasma barrier), instead of a metal (for example, being one of the rare materials that will usually reflect RF regardless of wavelength) reflecting almost all of the energy, that same material will suddenly reflect virtually none of the energy. Note that this will apply to frequencies that SHOULD reflect off a given material.
TBC
(CONT)
DeleteRegarding multiple signals: multiple sources (sufficiently spaced) and multiple receivers will, of course, increase the risks of being detected. This is true regardless of the physical configuration of the stealth asset.
Once again, Stealth is NOT guaranteed. Ever. There are ALWAYS conditions under which an asset might be detected. Military planners considering stealth options consider numerous factors, depending upon specific scenarios, and the specific intelligene gathered concerning any party that might become involved.
OTOH, there are configuration issues that are as problematic for the would-be hunters. No one has, or will ever have, unlimited resources. Building, deploying, maintaining, and operating detection assets draws from these resources. Resources applied to these functions are not available for other functions... like farm machinery, transportation infrastructures, weapons and deffence developement, communications infrastructures, housing, etc.
BTW:
IIRC, the 10^-17 W/m^2 limit figure was specifically presented in terms of IR detectors. This is a function of the theoretical limit imposed by the number of actual photons emitted at a specific frequency, and by the amount of "noise". The absolute limit is the point where there is only a single photon available to strike the detector, assuming that a single photon can produce motion in a single electron. This is combined with the noise limit. The limit is usually expressed in terms of electrons. Thus, theoretical limit is the point where there is activation of a single electron. Current noise limits are at about 5 to 10 electrons (readings less than this are unreliable). This means that for the specific IR wavelength in question, 10^-18 W/m^2 would be the theoretical limit. UV detectors are much less sensitive, because much more energy is bound up in the single photons. However, existing, rather cheap, RF detectors would already be much more sensitive than this. Additionally, this figure made other assumptions, such as a 1s exposure window.
I bring this up because, again, the thread I have been addressing here has never been about whether or not it would be possible to detect an asset with a sufficiently powerful RADAR (or LIDAR, or other equivalent method), but about which configuration is preferable for stealth applications: sharp reflection or diffuse reflection.
Yes, of course, the reflected signal will be uch less for diffuse reflection. My point, however, was that diffuse reflection will effectively guaranty that photons WILL arrive at a detector, regardless of position. Notably, the reflection will arrive at the location of the source.
Hunters will make decisions based upon sets of conditions such as optimal ranges. They will also take into effect all of the possible stealth considerations. You can enhance probability of detection by increasing the amount of energy. You can determine the likely ranges where transparency due to plasma barrier will become a problem for likely materials, and scan at intensities approaching this limit. You can also increase signal duration: with a floodlight approach, you can transmit constantly; or, with a ranging approach, you can transmit for as long as it takes a photon to reach the inner defined range. Either way, this multiplies the probability of detection. You can also increase the size of the detectors, and/or increase the exposure time frames. You might have to expend incredible amounts of energy, and you might have to wait for hours or days... but if there is a signal being projected in your direction, you WILL receive it.
But you can't see what is not there. Directed reflection is no guaranty that you will avoid detection, but it is the only way to avoid a guaranty that you WILL be detected by an appropriately configured platform.
TBC
Regarding my point about signal separation: I was refering to original and reflected signal separation, NOT resolution between different sources.
DeleteThis does NOT apply to all conditions.
Coding won't help because the reflected signal will retain the same coding.
The principle problem addressed here is for a target that is in near alignment beteen the source and the receiver. Ideally, the target will be in the signal cone, but will project toward a receiver that is outside of that signal cone, with the receiver registering only the reflection off the target. However, there is a possibility that the reflection might be directed toward a receiver that is in the original transmission cone.
Under most conditions, this would not matter, because the receiver would take in both signals, and would be able to eliminate the signal from the original source. However, angular resolution is an issue. Longer wavelengths have progressively poorer resolution, as a physical limit. Thus, it is entirely possible that the reflected signal will appear from the same direction as the source, and it will be impossible to resolve the two.
This also happens if the original signal has a long enough wavelength that it diffracts around the target, rather than being reflected by the target. It also happens if the target is transparent to the wavelength (non-metals, long RF wavelengths).
Sorry, I think I need to correct a statement. The plasma barrier (this might be "plasma LIMIT", I forget the exact phrase) for Aluminum should be written as 18 eV, NOT 18 mV.
DeleteOkay then.
DeleteLet's see, laser spot size equation is 1.2 * Distance * Wavelength / Lens Diameter. We want a diameter of 1.12 billion km and have wavelength as 400nm and lens diameter as 1m, we need to work out distance. I get distance: 1 * 1.12 * 10^12 / 1.2 * 400 * 10^-9 : 2.33e18m or 2333 trillion km.
My number was off by a factor 2000.
To work out the angle, I'd use this calculator (:http://www.cleavebooks.co.uk/scol/calrtri.htm) and get an angle of 0.00138 degrees. I think that translates to 5.98e-6 degrees^2.
I agree with your assessment that you would not want to try diffusing the LIDAR signal in all directions even with a very low reflectivity surface, because even a factor 1000 reduction in return signal would just lower the detection range from trillions to billions of kilometers.
On the other hand... let us imagine that the LIDAR target has a perfectly hemispherical face and is coated with Vantablack that absorbs 99.965% of the incoming wavelength. The Vantablack yields a signal reduction factor of 2857. The signal power being bounced back by a hemispherical depends on the size of the sphere and the distance, so let's fix the distance and find the signal reduction factor. At 1 billion km, the 400nm laser beam has spread to a diameter of 480km. If the target is 480km wide, it would project the bounced signal onto a sphere with a radius 1 billion km, so the signal reduction factor is 1000000000^2/480^2: 4340277777778. The return signal strength of a 10MW beam would be 8.06e-10W/m^2. A sensor sensitive to 10e17W/m^2 of radiation would be able to pick up this signal after it has been spread out over 80600000m^2. This is a disk of diameter 101.3km. I'm not sure which 'virtual laser' parameters I need to use to find the distance required for the 400nm beam to spread out to that spot size. Do I use a 1m focusing lens? If so, the distance becomes 211 million km.
That's still a lot, but it's not across-the-solar-system distances. If we factor in a more natural spaceship size, like 10m diameter instead of 480km, it would only intercept a factor 10^2/480000^2 of the incoming signal. This would further reduce the detection distance by a factor 2.3 billion.
If I re-done all calculations with the LIDAR being emitted from 1 million km instead of 1 billion km, the spot size at the target becomes 480 meters, the signal is reflected into a sphere 1 million km in radius and the 10m target intercepts 10^2/480^2 of the incoming signal. Add in the Vantablack, and a we get a signal reduction factor of 2857*(480^2/10^2)*(1000000000^2/480^2): 28570000000000000000. A 10MW signal gets reduced to 3.5e-13W/m^2. A sensor able to pick up 10e-17W/m^2 can detect this after it has spread to a disk 105km is diameter... which corresponds to a distance of 218 million km?
I could be entirely wrong about how I calculate the separation between target and sensor, but I am right about the signal strength reduction factor. It doesn't seem too bad.
I'll get to the rest later, but I just wanted to make the point for now.
I don't have a lot of time, so I'll have to do this in parts again.
DeleteI am still getting quite different results on the angle of diversion. Looking at the calculator site, I might have an idea of what the problem is, although I don't know if it would account for the size of the error.
Remember that the final "spot" is going to be projected onto a sphere, with all photons travelling equal distances for an equal time. Your online calculator, however, is trying to calculate this angle onto a flat plane.
What I have done is to divide the diameter of the projected "spot" (as the length of an arc) by the complete circumference of a circle at the given distance. Here, the distance is 2.333 * 10^15 (2333 trillion km).
Thus, 1.12 billion km / (2*pi*2333 trillion km) gives us the ratio of the two arcs. We then want to convert this ratio into degrees, so we multiply the result by 360 (the above ratio equals n° / 360°).
The actual resulting figure is greater than my previous calculations, but it is still in the same order of magnitude of 10^-5°. This would translate to an order of magnitude of 10^-10 °^2.
I believe you have made an error in your distance reduction calculations. Your 2.3 billion reduction factor (for the 10m hull rather than the 480km hull) appears correct for the energy flux reduction. However, the distance reduction would be the square root of this figure.
DeleteNote that, for the same reson, your VantaBlack signal reduction factor would not apply to range. Instead, the range reduction factor would be the square root of the signal reduction factor. This would be a range reduction of about 50 or so. Not much more.
DeleteOTOH, you appear to be translating this into the reduced area footprint anyway, so your final range value is probably more or less correct.
DeleteThat said, keep in mind that the VantaBlack and reduced cross section reductions apply under BOTH scenarios. This means that the angular reflection intensity to be reduced by exactly the same factors. Granted, full reflection will have a much smaller range (for equal detection conditions), but it will not change the comparative chances of detection.
DeleteIt is also worth noting that a signal strength of 10^-18 does NOT mean that it is UNDETECTABLE by a receiver rated at 10^-17. The receiver STILL has a 10% probability of detection at this level. Signal densities are not truly uniform. They are probabilistic. The photons are still there to be detected, and COULD still have a localised density sifficient to overcome any noise.
I need to keep track of the topics here!
DeletePhysical network of sensors: We must take into account the effect of field of view. Although a 1 degree square signal will maintain that size despite expanding over billions of square kilometers, we do not need thousands of sensors per target. A decent field of view would allow them to detect signals from large volumes of space. If placed far away enough, only the strict lower requirement of 40000 or so would be necessary for the entire solar system.
Signal reduction factor: I might have made mistakes with my geometric calculations, so let's try again with purely W/m^2 calculations. We'll suppose that the emitter and receiver use the same LIDAR dish of 1m^2 and are placed on the same vessel. Perhaps we can can get a detection equation dependent on distance out of these calculations.
We emit from a 10MW/m^2 source at 400nm. We'll note this value as I for intensity. Wavelength is W, Lens diameter is L. At a distance D, the beam has spread to a disk of diameter 1.2*D*W*L, which we will note S for spot size. The intensity has been reduced by a factor F1 = (0.5*S)^2*3.14 =[(0.6*D*W/L)^2*3.14].
For D=10e9, W=400e-9, L=1, we get F1 = 180955.
The target only intercepts incident light equal to its cross-section in the laser disk. For a spaceship of roughly circular cross section with a radius R, it will intercept R^2/(0.5*S)^2 of the incoming light. This gives us a signal reduction factor F2 = (0.6*D*W/L)^2/R^2.
For R=5, we get F2 = 2304.
The surface coating that reflects the LIDAR beam will not return all of the energy. An extreme black surface like Vantablack might absorb 99.965% of the incoming energy, which we will not A = 0.99965. This gives us a third signal reduction factor F3 = 1/(1-A).
For the Vantablack mentioned above, F3 = 2857.
Finally, this signal gets bounced back to the source. Since we care about the W/m^2 figure, I figure that we only need to calculate the radiations of a single square meter of reflecting surfaces. It diverges at the same rate as the incoming beam for a flat surface, but a rough, bumpy or hemispherical surface will emit in different directions. We'll note the effect of the surface's geometry as K. The fourth signal reduction factor F4 is therefore equal to (0.5*S)^2*3.14*K =[(0.6*D*W/L)^2*3.14]*K. This is because we are assuming emitter and receiver are at the same distance.
For K=1, we get F4 = 180955.
Putting all these equations together, I obtain the signal strength (G) received by the sensor. It is equal to I/(F1*F2*F3*F4). We can further simplify it at I/(F1^2*K*F2*F3).
G = I/{[(0.5*S)^2*3.14]^2*K*[R^2/(0.5*S)^2]*[1/(1-A)]}
Writing out the F1^2*K:
G = I/{(0.5*S)^4*3.14^2*K*R^2/(0.5*S)^2*1/(1-A)}
Simplifying the (0.5*S)^4/(0.5*S)^2
G = I/{(0.5*S)^2*3.14^2*K*R^2*1/(1-A)}
Rewriting the division 1/(1-A) and 3.14^2:
G = I/{(0.5*S)^2*9.869*K*R^2/(1-A)}
And finally:
G = [I*(1-A)*0.10132]/[(0.5*S)^2*K*R^2]
If we rewrite 0.5*S as 0.6*D*W/L, we get
G = [I*(1-A)*0.10132]/[(0.6*D*W/L)^2*K*R^2]
If we input I:10e7 W/m^2, A:0.99965, D:10e9m, W:400e-9m, L:1m, K:1, R:5m, we get G = 2.4626e-4 or 0.246mW/m^2.
From this, we can work out whether the object is likely to be detected by comparing G to the sensitivity value the LIDAR is expected to have. For the values we inputted, detection at 1 million km is certain.
We can also determine that increasing the emitter/receiver dish has a squared effect on detection distance, same as reducing cross-section radius.
I'll get back to the rest later, I promise.
Before addressing your new comment, I have a few more observations from the previous comment.
Delete*First, it took a while for me to decypher your paragraphs. It wasn't entirely clear that you were making a comparison between the tight beam reflection and full field reflection for each case. originally, it looked like you were defining a beam strength at a given distance, and then using that information to (incorrectly) determine the range. Instead, I find that:
*Second, you are comparing the range of the tight beam reflection with the intensity of the full field reflection at a given range. This does not yield an honest comparison.
To be fair, I fully conced that the full field reflection will have a MUCH more limited detection range than the tight beam reflector, FOR A GIVEN DETECTOR. This is actually obvious, because the same amount of energy is spread out over a wider field.
You can actually quantify the reduction factor quite easily. There duction factor, in terms of range, for the full field reflector (as opposed to the tight beam reflector) will be the slightly less than the square root of the angular area of a sphere divided by the projected angle area of the reflected beam. For example, a millimetric RF, with a tight beam reflection of 1°^2, will produce a reduction factor in the range of 30 000 ^-2 to 40 000 ^-2 (maximum of about 200). For the 400 nm LIDAR, the range reduction factor would be in the order of magnitude of 10^7. So, yes, quite significant.
Note: the angular area of a FULL sphere is NOT used in the equation (which would otherwise yield a result of slightly MORE than 40 000), as it is not possible for the reflection off of a hemisphere to cover a full sphere; although it WILL cover significantly more than just a hemisphere (relfections off the "terminator" will approach 90° off the original beam, leaving a shadow the size of the object).
*Third, regarding your question about the "focusing lens" parametres:
My understanding is, assuming that the incident spot size at the reflector is larger than the reflector itself, the dimensions of the reflector replace the original waist calculation. I am not certain whether this will be the actual dimension of the panel, or the dimension of the reflecting cross-section, but I suspect the former.
If the incident spot size is smaller than the reflecting panel, I see three possibilities. The first is that the size of the panel (again, either actual dimensions or cross-sectional dimensions... I suspect the former) will determine the new divergence calculations (this does not sound right to me, though). The second option is that the actual size of the reflecting spot will be the basis for the new calculation (I can not see why this would be the case, but it is possible). The third option is that the beam will follow the divergence constraints of the original waist size (this seems the most likely option for me).
In any case, a saturated reflector should behave as a completely different emitter, so it should not be possible for the beam to be reflected with the same divergence if it saturates (or otherwise extends beyond the boundaries) of the reflcting surface.
"We must take into account the effect of field of view. Although a 1 degree square signal will maintain that size despite expanding over billions of square kilometers, we do not need thousands of sensors per target. A decent field of view would allow them to detect signals from large volumes of space. If placed far away enough, only the strict lower requirement of 40000 or so would be necessary for the entire solar system"
DeleteActually, if you read carefully, I never said that you need 40 000+ platforms PER TARGET. Rather, I said that any given point in space will require 40 000+ sensors (assuming emission windows of 1°^2, which I later identified as millimetric RF). Yes, of course, these sensors will each be covering many different points.
However, you need these platforms to be in the correct windows.
*Platforms will be in orbit. This means that they will move in respect to one another. This, in turn, means that you will require additional platforms to cover the zones as other platforms move out of position, for coverage of a specific region in space.
*Likewise, since it is impossible to configure an arrangement where all platforms cover all zones for all possible regions in space, you will need additional platforms to fill in the gaps of coverage for specific regions in space. That said, so long as you don't have long strings of gaps in the same zones, it won't actually be all that important to cover every possible gap... but you ARE going to have multiples of that 40 000 base figure.
In short, I have only said that 40 000 platforms would be a MINIMAL coverage figure, and NOT 40 000 per target.
BTW:
DeleteRemember that this minimum figure is based on the size of the emission (reflection) window. For a 400 nm LIDAR, you will need a minimum of 10^10 platforms tfor full coverage of a given region. If the target has a saturated face with a linear dimension of 10m, that minimum gets bumped up to 10^12 platforms.
"We can also determine that increasing the emitter/receiver dish has a squared effect on detection distance, same as reducing cross-section radius."
DeleteIf I am reading this statement correctly (which is entirely possible), this is actually wrong.
For clarification:
*The range will change as the square root of the detector area. If you increase the area by 4x, the range will increase by 2x. If you increase the area by 9x, the range will increase by 3x.
*Similarly, the range will change as a function of the square root of change in signal strength. 9x signal strength yields 3x range.
Again, perhaps that is what you meant to say.
Your foumula tree appears accurate.
DeleteFor our purposes, we are mostly interested in F4, as it is the only factor that changes between the two conditions being discussed. I am assuming that K is also taking into account the dimensions of the reflecting plate, as this will also affect the distribution, in addition to shape.
I might have to try to work on a few renderings to demonstrate the problems with assuring coverage. The problem is, I am not certain how I could arrange to do that... I don't know if the images will paste properly.
A note for your scenario setting the formula value of K=1:
DeleteI assume that this is for a tight beam with reflection divergence being equal to source divergence. That being the case, if your figure is correct, it argues against your claim that a single set of platforms could cover the entire solar system (even ignoring the fact that once you move from a zone of optimal coverage, your start creating zones with overlapping coverage and gaps). One million km is only 1/150 of a single AU. Thus, if you start applying methods like VantaBlack, you are going to need to multiply the base coverage by factors in the order of hundreds, or even thousands... without taking into account the addtional units required to cover for the gaps I mention.
It is worth noting that there IS one factor that helps reduce the total number of platforms required. Notably, any asset will have to eventually pass through a number of zones. For a well established network, it is unlikely that any gaps in coverage will occur in the same angular region (respective to the asset) in all zones. This means that you might do okay with even 10% probability coverage, if the asset has to travel through dozens of zones.
DeleteThere is some risk with this, of course. With the resulting intermittent coverage, it can be difficult, if not impossible, to identify if you are tracking a single asset, or if you are dealing with multiple assets operating it relatively close proximity (within adjacent zones of arbitrary size).
BTW:
DeleteI have been actually been assuming that both detection and transmission platforms are capable of full spherical coverage, either through the presence of multiple units, and/or the use of scanning. Note that the latter option adds some inherent problems that could further limit detectability.
I might have to write a dedicated 'how to deal with active detection' in the future.
DeleteFor now, I've found that K=1 is not necessarily true in the majority of cases. It can be incredibly small for short wavelengths reflecting of an extremely smooth hemispherical surface. It can become very large for certain radio wavelengths reflecting off an object with a large RCS.
Also, radio sensitivity seems to follow different standards than optical sensitivity. Instead of W/m^2 values, all I can find is decibels, which implies that if the sensor platform is sufficiently shielded from unwanted radiations, then it can detect radio signals a few billionth W/m^2 above the universal background radio signal!! It makes a strong case for radio stealth only being really achievable with counter-electronic warfare measures, such as decoys, jammers and spoofing. To be further investigated.
Yes, K=1 would probably be a rather rare exception. However, it is probably about as good as any other single value for a single case scenario.
DeleteFor clarification: I was assuming that K was addressing ADDITIONAL divergence factors, assuming a specific given wavelength (in other words, assuming a fixed value for lamda, it addresses reflector specific conditions that could modify the divergence). I made this assumption because F1 already appears to take divergence into consideration. Thus, I don't think that the wavelength values in this most recent post are relevent to K value variations.
For K=1, the divergence of the reflected beam should be the same as the incident beam, which is the value dependent upon wavelength. Instead, variations leading to 1>K would probably tend to be the result either of (convex) lensing (a beam passing through uneven transparent/translucent layers), or larger reflecting surface area (same as using a larger mirror for the original beam). Variations leading to K>1 would result from from rougher surfaces (diffusion effects), concave lensing, reduced reflecting area, etc. K=1 would probably require an absolutely smooth, polished surface.
It isn't exactly a "different standard", as such. There are benefits and drawbacks to RF. An important drawback is that useful imaging resolution is virtually impossible at any meaningful distance. Another important drawback is that non-metallic materials tend to be transparent/translucent to large swaths of RF. Even metallic materials become increasingly transparent.
One benefit is that you have MUCH less energy per photon. Therefore, the photon flux for even very weak RF signals tend to be huge. This means that detection ranges can be huge (unfortunately, this doesn't work so well for DAR sensors, because of the decreased reflectivity of RF).
A second important benefit is that RF is generally not subject to blackbody interference. Most blackbody emissions begin in IR ranges. Although very intense BB emissions can expand into RF wavelengths, the actual photon flu from such emissions are still relatively weak, especially for longer wavelengths. This means that the receiver does not have to be colder than the source to avoid interference. All this is because RF emissions are produced by different means. Again, it is not because they don't behave like other photons.
Addressing radio stealth: it is still quite viable. RADAR stealth is viable, even with powerful transmitters, because of the habit of RF to transmit THROUGH materials, rather than reflecting. Thus, it is actually rather difficult to get a good detection signal (especially if anything reflected is going in the wrong direction). Direct radio stealth is achieved by restricting radio emissions. RF is generally not produced by BB radiation, except at the very highest intensities... and even then the emission levels are fairly low. This means that you need to generate it through other means to be detected... and this is fairly easily shielded because, although most materials are rather poor at reflecting RF, they tend to be much better at absorbing RF.
@ Mikkel Haaheim
ReplyDeleteUnder normal circumstances (like here on Earth) a network of 40,000 sensors would be difficult to establish, but in the space environment something like that might become trivial.
I suggest you look up the "Server Sky" concept of Keith Lofstrom (yes, that Keith Lofstrom), where small computer chips backed by equally small solar cells are floating in free space to establish what is essentially a massively distributed computer network (http://server-sky.com). Individual chips are cranked off the assembly line relatively cheaply these days, and it can be assumed that a space civilization will have at least that level of ability as well.
Planets. moons and asteroids will likely have a Server Sky network in orbit to deal with the large scale computational needs of the polity or planet, and other Server Sky clouds can be expected in stable orbits in places like the Lagrange points in various orbits. Whoever controls the Server Sky platform or has access to it could conceivably have millions of sensors built into these chips and be able to generate finely grained 3D views of the surrounding space. If they have access to multiple server sky clouds (for example Earth might have one in GEO, plus ones at L1, L2 and L4 and L5). Other polities might not have the same density of coverage, but it will still be considerable.
I don't know why you would want to expose your computing hardware to the cosmic rays, thermal variations and general harshness of the space environment, when you could instead use the distributed satellite network as a simple communications network while keeping the computing hardware on the ground...
DeleteAs for the 40000 sensors number, using longer wavelengths that diffract faster and compensating for the loss of power by using the 100MW+ power supplies meant for laser weapons can drastically reduce this requirement.
@Thucydides
DeleteI will address this when I have the opportunity.
Actually, it is MUCH easier to deploy such platforms on Earth. First, because you wouldn't have to worry about most of them moving out of position. Second, because you wouldn't have to expend extreme amounts of energy to deploy them, nor to access the for maintenance. Third, because they would be better protected against the majority of natural threats. Nor is there any reason why you would not be able to deploy the same wafer tech that you would use in space.
DeleteThe only real limitations are that planetside arrays can not cover the vast amount of space required to detect objects light-minutes away, and that the same atmosphere that protects the platforms from harm will also tend to block out certain wavelengths of photons, and other sources of detectable energy.
The problem with the Server Sky approach is that it does not really address the actual problem. Yes, you need great numbers of platforms/arrays... but these can not just be put anywhere. You need a large number of platforms at the right locations.
Server Sky might make an exceptionally competent array that would serve far better than a single massive platform. However, the reality is that you would then need 40 000 of these ARRAYS, and these arrays would only be able to assure coverage over a specific point. The further removed you are from this "ideal" point, the more you suffer from overlap and gaps in coverage, requiring even more arrays to cover those gaps.
From a tech standpoint, the arrays would be much better performing than single massive platforms. However, there are certain liabilities to take into consideration.
First, all of the units will need to communicate with one another, or (at least) with a centralised control relay. Now, this is also true of microchip components; however, at the distances involved, you no longer have the option of fixed pathway guides that define which units are communicating with which other units (requiring info to be location tagged, which complicates processing requirements cinsiderably). You also have an increased amount of signal activity that could result in network, processing, and sensory interference. Furthermore, although photons travel much faster than electrons, this advantage is largely dampened by the distances involved, as well as the (current) need to encode and decode the photon signals into electron signals that the unit processors can perform operations with.
Second, although the site addresses the most common processing problems associated with radiation exposure, it does not currently provide fixes for all of these problems. More importantly, it does not address the primary damage that radiation can cause. Here, I am refering to transmutation, neutron embrittlement, physical radiation "burns", and other sources of physicl damage caused by alpha partical, beta partical, neutron, and osmic radiations that could easily render such thin strata microcomponents unusable.
Third, although the site addresses the issue of avoiding physical damage due to collison hazards from other assets and debris, it does not address the issue of micrometeoroid damage. IIRC, analyses conducted on the micrometeoroid protection layers of the apollo space suits revealed that micrometeoroid impacts can be as frequent as dozens to hundreds of impacts per second per m^2. These impacts often penetrated as far as a few mm into the protective layer. An unprotected chip measured in microns are unlikely to survive such an environment for any meaningful length of time. Furthermore, the avoidance parameters against debris collision suggested by the site would not be available in some of the locations where coverage would be required.
@Matter Beam
ReplyDeleteThe 40 000 sensor figure addresses the number of 1°^2 windows that would need to be covered (for a total reflection divergeance of 1°). Amplitude is irrelevant to this base figure, which essentially assumes infinite range (or, in other words, assumes that the platforms are already in the arbitrary range limit).
This is a MINIMUM platform requirement for the given condition. The requirement is increased dramatically for Gh or greater frequencies (millimetric or lesser wavelengths). The requirement would, of course, increase for more limited ranges. It also increases for targets that move outside of an optimal position, or for platforms that move out of position due to differing orbits.
Using longer RF wavelengths DOES decrease the number of required platforms. However, there are other considerations that yield such RF frequencies less suitable (RF transparency, for example).
OK, I started writing the space opera novel (with heavily armored battleships having glowing dust plasma wings firing gauss cannons and deploying casaba howitzer missiles with HEAT warheads yay!) and I needed to come up with an alternative to dust plasma radiators for another competing faction in the storyline (this other faction uses genome manipulation instead of physics based tech).
ReplyDeleteI asked this on the worldbuilding forums on stackexchange and one contributor suggested this:
https://spectrum.ieee.org/tech-talk/green-tech/solar/passive-radiators-cool-by-sending-heat-straight-to-outer-space
A passive radiator that shunts heat directly into space. Could this be possible?
Also, what about liquid or gas transferred thermo electric generators?
The link is blocked to me for some reason, but this is already the principle of operation of a radiator: it radiates heat to outer space. This is the only way to get rid of heat for a spacecraft, actually. Apart from using a heat sink, but this is a temporary solution as at some point the heat sink will be filled/depleted.
DeleteAs for thermoelectric generators, they work on a heat gradient: you have a hot object, a cold object, and heat flowing between those can be partially tapped for energy. But at some point, you have to get rid of the heat in the cold object or it heats up and there is no gradient anymore. This is what the radiator does.
Note: you could use colder radiators have a bigger heat gradient and thus more energy, but then the colder radiator have to be much, much bigger to get rid of the same quantity of heat.
Now, when you are relaxing the standards and allow not-too-hard SF, little bits of magic can help. For example, the ~100% efficient torch Epstein drive of the Expanse. Similarly, you can have sort-of magical ~100% efficient weapons.
You can also decide that your FTL gizmo allows for dumping heat directly into hyperspace somehow - be careful with the implications, though, such a system probably many, many secondary applications that will have to be carefully thought out.
Congratulations!
DeleteI have a solution to your question, with the added bonus of fitting within the 'gene tech' theme: spider silk radiators.
This is a variant on the wire-loop radiator concept described in 'All the Radiators'. Thin wires are dragged through a heat exchanger, absorb heat, then radiate it as they are rolled into the vacuum of space like a clothes line.
Thinner wires have better surface area to weight ratios, so their performance improves. High specific strength materials can allow for very very thin wires strong enough to remain under tension while the spacecraft accelerates. An example is genetically modified spiders drinking carbon nanotube-laced water and producing very strong spider silk. It can be spun into fibers and used in wire loop radiators.
Great suggestion!
DeleteHow vulnerable are these spider silk radiators in combat though? If they are, could they be retracted and the bioship ends up spewing out super-heated water to cool down during battle instead?
Pretty vulnerable. The material is strong and flexible but such thin strands are probably weaker than wet paper.
DeleteThe good thing though is that a liquid tank of spider silk can unspool the strands for months on end. 1 ton of silk 'goop' can be dried and wound into 976 million km of micrometer spider silk wire.
OTOH, the thin strands would be much more difficult to hit; and, the fact that they would only be anchored on one side, and would be extremely flexible, means that they would be morely likely to "give" under impact, rather than to break or tear. So this is probably a rather useful idea.
DeleteYou probably don't need to drag the filaments through the radiator, either. If you allow the strands to "drip" ("stream" would probably be more accurate) out into a natural taper, thermal conductivity/emissivity should allow the waste heat to distribute itself down the line. The effect would be similar to demonstrations of wafers that melt and cut through butter simply by conducting the body heat of the person holding the wafer.
Actually, this leads me to a variation of the liquid droplet radiators. One suitable example for this discussion is the cooking of sugars to the "string" stage. The result is a very thin strand of high viscosity liquid. So, use some kind of sugar molecule (or something similar) as the base of the coolant loop, and let it stream out into long threads that are MUCH easier to collect than individual droplets.
The wire radiator variant anchored only on one side uses centripetal force from spinning loops to hold them in position. The wire variant I was describing is one where physical support structures pull along the wires and hold them under tension, like belts and pulleys. It would be much more robust against stresses and damage but the mass of the extra equipment suggests it works best when bunched together in 'bands'.
DeleteYour idea sounds more like a conventional liquid droplet radiator where strings are used to move the droplets around, like a series of elevators.
I seriously doubt that sugar-based or viscous liquids will hold up to the temperatures that radiators operate at, but I understand the analogy.
Working in reverse:
DeleteThinking about it, actual sugar based variants probably would not work very well, unless you had a synthetic sugar with an extremely high melting point. Also, you are quite correct that viscous liquid strings could never offer the same temperature performance as droplets. However, there are other issues to consider. Most imprtantly would be coolant retention. Isolated droplets are extremely vulnerable to mass flow loss due to droplets that escape from the collection field. The liquid strings don't actually HAVE to hold up under temperature. It would be fine (and expected) for the strings to break. The benefit is that you would need less coolant mass because even the broken strings would be much easier to recover than free drifting droplets. Keep in mind that the strings will most likely break toward the point of highest temperature, which would be the source. Once they are sprayed, there will be no further tension on them to break them... until they reach the collector and are reeled in, at which point the temperature would be much lower, and the structural integrity much stronger. Any molecules that are not on course would be towed back toward the rest that are moving toward the collector.
Yes, the sugar string concept is a variant of the liquid droplet concept. My notes on the spider thread concept were based first on the loop/belt radiator, assuming either a free-floating belt (except for the anchor point where the loop passes through the heat exchanger; note that this would require a circulation wheel running at sufficient speed that the inertia within the fibres is sufficient to encourage the sheets to flow to the maximum extent, rather than for the fibres to get bunched up --think about how you would through out the end of a blanket to have it drop flat on a bed), or having loops relying on the centrepetal force. Later, I incorpared the idea of free-floating strands that were not cycled through (extending out more like tapered antennae).
I agree that the idea works better when grouped in bands or sheets. However, the strands in the bands do not need to be anchored (or tied) to one another.
I have an idea. Scale up the strings a bit and incorporate piezoelectric elements acting on microscopic surface elements. These surface elements can be actuated to switch between a superhydrophilic and superhydrophobic surface - I am not sure how, but tiny moving 'hairs' might be the solution.
DeleteThe string is in a superhydrophilic state when it picks up the liquid droplets. The droplets easy slide up its surface due to surface tension. They stick to the string as it is pulled along. At the collection point, an electric current it run through the string and the hairs rise, creating a hydrophobic surface. The droplets ball up and fall off, allowing them to be collected.
If you are going to combine the string with the droplets anyway, there is really no reason to cycle the string. Simply suspend the string between the spray and collection points. No need for drive motors, nor fancy switching systems. The problem here, though, is that the strings now become an essentially dormant part of the structure. You are adding mass, and it now actually matters somewhat if the strings break.
ReplyDeleteThe benefits of the "string stage" coolant are:
*less coolant loss than droplet radiators (greater control over molecular vectors, and greater retention following stray impacts, as stray molecules in both cases will be pulled back into position through molecular bonds in string... or even by simply surface tension in contiguous string segments with broken molecular bonds)
*easier to configure threadsinto sheets with optimum molecular density (contiguous monofilament)
*less mass than wire or even spidersilk radiators (whether on loops or strands)
*superior performance to wire or spidersilk radiators (due to relaxed temperature limits)
*simplified operating principals
*less vulnerable to damage than wire or spidersilk radiators
The only real downside is that it does not perform as well as droplet radiators, due to even relaxed temperature limitations. However, this is likely well compensated for, given that there is likely to be much less coolant loss (causing better mass reduction) and better control over optimal densities for best performance (it can be really difficult to get optimal densities in droplet flows, especially since droplets that are too closely packed could easily ick each other out of their vectors toward the collectors).
what's percentage of droplets evaporate,lose and can't be collected,i mean,many droplets can't renter the radiator's recycle,they disappear forever
ReplyDelete